【深度學習】：【結果衡量名額】召回率（Recall），精确率（Precision），F度量（F-measure），Map，ROC，AUC

精确率（Precision），又稱為“查準率”。

召回率（Recall），又稱為“查全率”。

召回率和精确率是廣泛用于資訊檢索和統計學分類領域的兩個路徑成本，用來評價結果的品質。其中召回率是是檢索出的相關文檔數和文檔庫中所有的相關文檔數的比率，衡量的是檢索系統的查全率。精确率是檢索出的相關文檔數與檢索出的文檔總數的比率，衡量的是檢索系統的查準率。如以下公式所示：

召回率(Recall)      =  系統檢索到的相關檔案 / 系統所有相關的檔案總數

         精确率(Precision)   =  系統檢索到的相關檔案 / 系統所有檢索到的檔案總數
           

下面這個例子可以有助于對精确率和召回率兩個概念的了解：

在一個資料庫中有1000個文檔，其中有100個是與NBA相關的，系統檢索出75個文檔，其中，隻有50個是與NBA相關，此時：

精确率 = 50 / 75 = 67%

召回率 = 50 / 100 = 50%

上面的檢索為第一次檢索，同樣的環境下改變檢索技術後進行第二次檢索，系統檢索出150個文檔，其中，90個是與NBA相關的，此時：

精确率 = 90 / 150 = 60%

召回率 = 90 / 100 = 90%

我們發現，精确率和召回率是互相影響的，理想情況下肯定是做到兩者都高，但是一般情況下準确率高、召回率就低，召回率低、準确率高，當然如果兩者都低，那是什麼地方出問題了。


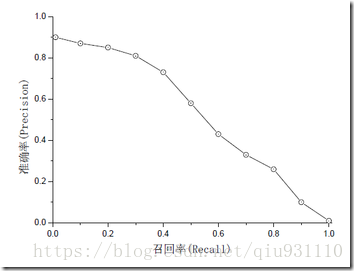
F度量（F-measure），結合精确率和召回率。

基于上文，不難得出準确率與召回率兩者基本存在一種“互補”的關系，簡單描述就有點像天平的兩端，你大我小，或者你小我大（這個比喻可能不是非常嚴謹）。是以在具體的應用當中，我們應該以哪一個名額為主呢？有沒有一個綜合的名額涵蓋了這兩個名額呢？此時，就需要引出F度量。F值的計算公式如下：

F 1 = 2 ∗ P ∗ R / ( P + R ) F1 = 2 * P * R / (P + R) F1=2∗P∗R/(P+R)

結合上文的例子，利用上述公式計算得到，第一次檢索的F1為57%，第二次檢索的F1為72%，顯然改變技術後的檢索效果優于改變前。

Map（mean Average Precision）

mAP是為解決P，R，F-measure的單點值局限性的。為了得到 一個能夠反映全局性能的名額，可以看考察下圖，其中兩條曲線(方塊點與圓點)分布對應了兩個檢索系統的精确率-召回率曲線。可以看出，雖然兩個系統的性能曲線有所交疊但是以圓點标示的系統的性能在絕大多數情況下要遠好于用方塊标示的系統。從中我們可以 發現一點，如果一個系統的性能較好，其曲線應當盡可能的向上突出。更加具體的，曲線與坐标軸之間的面積應當越大。最理想的系統， 其包含的面積應當是1，而所有系統的包含的面積都應當大于0。


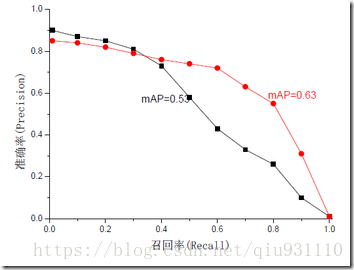
這就是用以評價資訊檢索系統的最常用性能名額，平均準确率mAP其規範的定義如下:(其中P，R分别為精确率與召回率)。


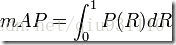
ROC（Receiver Operating Characteristic）

AUC（Area Under roc Curve）

ROC和AUC是評價分類器的名額，上面第一個圖的ABCD仍然使用，隻是需要稍微變換。

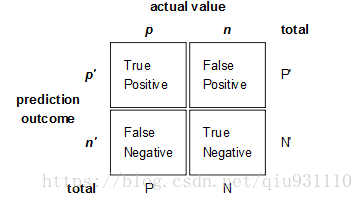 回到ROC上來，ROC的全名叫做Receiver Operating Characteristic。

ROC關注兩個名額

True Positive Rate ( TPR ) = TP / [ TP + FN] ，TPR代表能将正例分對的機率

False Positive Rate( FPR ) = FP / [ FP + TN] ，FPR代表将負例錯分為正例的機率

在ROC 空間中，每個點的橫坐标是FPR，縱坐标是TPR，這也就描繪了分類器在TP（真正的正例）和FP（錯誤的正例）間的trade-off。ROC的主要分析工具是一個畫在ROC空間的曲線——ROC curve。我們知道，對于二值分類問題，執行個體的值往往是連續值，我們通過設定一個門檻值，将執行個體分類到正類或者負類（比如大于門檻值劃分為正類）。是以我們可以變化門檻值，根據不同的門檻值進行分類，根據分類結果計算得到ROC空間中相應的點，連接配接這些點就形成ROC curve。ROC curve經過（0,0）（1,1），實際上(0, 0)和(1, 1)連線形成的ROC curve實際上代表的是一個随機分類器。一般情況下，這個曲線都應該處于(0, 0)和(1, 1)連線的上方。如圖所示。


用ROC curve來表示分類器的performance很直覺好用。可是，人們總是希望能有一個數值來标志分類器的好壞。

于是Area Under roc Curve(AUC)就出現了。顧名思義，AUC的值就是處于ROC curve下方的那部分面積的大小。通常，AUC的值介于0.5到1.0之間，較大的AUC代表了較好的Performance。

AUC計算工具：

http://mark.goadrich.com/programs/AUC/

reference