1 概述
對于機器視覺,我目前還是剛起步,可能步還沒起來。
近日開始接觸雙目Stereo的相關算法,主要是對Heiko Hirschmüller在2008年的文獻(Hirschmüller 2008)中描述的算法進行研究。該文獻,也就是利用互資訊(Mutual Information)作為計算matching cost的基礎進行stereo重建的工作,在相關領域内的影響還是比較大的。他所使用的cost aggregation的方法,也運用在了目前OpenCV(目前我使用的是3.4.1)中的SGBM方法中。這些日子試圖複現文獻中的算法,但是由于自己基礎薄弱,很多地方并不能完全了解和複現,這裡僅作為研究過程中的記錄,以備自己進行回溯以及與同行們的交流讨論。
在複現算法的過程中,使用OpenCV 3.4.1和C++編寫測試程式。程式運作在Ubuntu 16.04 64bit的系統上。OpenCV是在本地編譯為Debug版本,以友善對程式進行調試。
對算法的複現将分步進行,本文主要描述對Mutual Information相關數值的計算。
2 基本假設
為了簡化分析,現假設組成雙目相機的兩個相機是完全一樣的,并且已經進行過stereo calibration,所獲得圖檔已經是rectify過的灰階圖像,在OpenCV中,這些圖像的資料type為CV_8UC1。
3 Warp
為了計算matching cost,需要利用mutual information。根據(Hirschmüller 2008)在文中的描述,計算雙目中兩個圖檔的mutual information時,需要針對目前的disparity map,對其中一個圖檔進行warp處理。這裡這個“warp”卻也是我第一次遇到,辭典上有一個非常fancy的翻譯,叫“翹曲”。其實有“彎曲,扭曲”的含義。我們這裡通常可以定義雙目中左相機的圖像為參考圖像(不變),右相機的圖像為比對圖像,disparity map即代表右圖像向左圖像進行比對時,右圖像上每個像素與左圖像上最佳比對像素的水準(x)坐标差。原文要求我們在計算mutual information時,需要對右圖像進行warp處理。所謂warp處理,就是對于左圖像中的每一個像素(x1i, y1i),根據目前的disparity map,在右圖中找到與之match的像素(x2i, y1i),從右圖中将這個像素取出,放入一個新圖像(warped image)中的(x1i, y1i)位置。這樣就可以得到一個warped image。計算mutual information時,将使用左圖像和這個warped image進行,而不再使用右圖像。
這裡實際上存在一個問題。原文并未指明如何進行warp,尤其在左右圖像match時對無法得到disparity的像素如何處理。首先,由于左右相機在拍攝同一場景時必定存在一個overlap,這個overlap一般情況下不可能達到100%的FOV(Field of View),在不存在overlap的像素區域,不存在disparity。這個情況原文并未給出處理方法。其次,在實際進行disparity計算中,對應于某些處于overlap區域的像素,優化算法仍可能給出disparity不可靠的結果,并最終認為該像素不具備有效的disparity。對于無disparity結果的像素,原文也未給出處理方法。
我目前采用了naive的方法:對于右圖中無disparity的像素,不對其進行warp,保留其在原始位置。這種處理方法并不一定正确,并且暫時無法保證像素覆寫的情況。後面需要進行優化和處理。
4 Joint Entropy and Mutual Information
原文指出,計算mutual information的關鍵過程是對joint entropy的近似。這可以總結為原文中的式(4)、(5)和(6)。
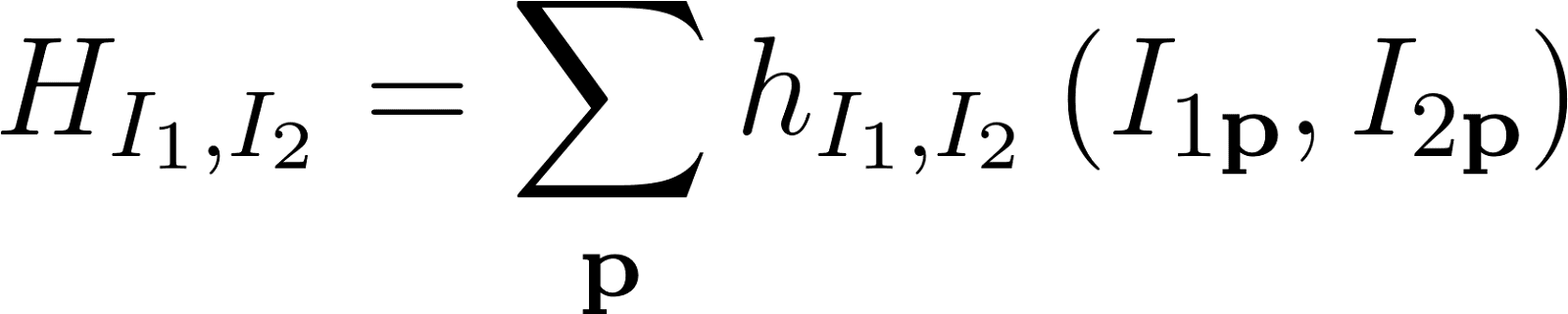
其中,HI1,I2即為joint entroy。這裡我花了蠻久時間了解它們。
首先需要明确的符号語言,I1和I2表示以intensity表示的左右圖像,而則I1p和I2p表示左右圖像上某個像素位置上的intensity。這裡I2表示warp處理過的圖像。進而HI1,I2為一個2D的資料,是一個2D表,這個表的次元是256x256。無論I1和I2自身的size是多大,HI1,I2的次元始終為256x256。
第二,原文式(5)中,對PI1,I2進行了2次卷積。卷積核皆為Gaussian kernel。由于我對機率統計方面的理論基礎很薄弱,花了很多時間試圖去了解式(5)的意圖。原文解釋第一次卷積是進行了一次Parzen estimation。所謂Parzen estimation實際是指Kernel Density Estimation (KDE)。KDE似乎是機率統計中很基礎的概念,是一種無參數化的機率密度估計方法。所謂“無參數化”即指在對随機變量的機率密度進行估計時,不指定機率密度函數的形式,而完全依賴所測得的實際資料。式(5)的第一次卷積即為進行了一次KDE,進而得到了PI1,I2的機率分布的估計。對于KDE的了解,可參考如下幾個網頁。
Kernel density estimation: https://en.wikipedia.org/wiki/Kernel_density_estimation
Kernel (statistics): https://en.wikipedia.org/wiki/Kernel_(statistics)
Can you explain Parzen window (kernel) density estimation in layman's terms?: https://stats.stackexchange.com/questions/244012/can-you-explain-parzen-window-kernel-density-estimation-in-laymans-terms
How to interpret the bandwidth value in a kernel density estimation?: https://stats.stackexchange.com/questions/226232/how-to-interpret-the-bandwidth-value-in-a-kernel-density-estimation
KDE與卷積運算的關系可參考
http://ieor.berkeley.edu/~ieor165/ 頁面上的第10講,Distribution Estimation。
原文式(5)的第二次Gauss卷積,真的沒有了解它的具體意圖。原文解釋是将KDE的結果進一步變為lookup table,然而我并沒有get到。
原文式(5)的計算中有兩個不确定的問題。第一,n的取值。n的取值我認為是圖像的像素總數(number of all correspondences)。第二,式(5)中出現了對數計算,這個計算不允許自變量為零。原文中也指出自變量不可以為零,但是實際情況中自變量很可能出現零,甚至是必然有零。原文推薦将零替換為一個較小的正數,以應适應對數函數的定義域。那麼多小算是“小”,原文并未給出。在後面的算法複現中,使用的值為1e-30。該數值實際上是随意取出的。在mutual information的計算中,我預計使用單精度的浮點數類型進行數值運算。在IEEE标準中,單精度浮點數能夠表達的數值範圍下限在10-38左右(Single-precision floating-point format ),取1e-30僅是一個個人愛好而已。然後需要注意的一點是OpenCV的版本問題。在2.x的OpenCV版本中,對于Mat對象的對數運算,其特性是與在3.4版本不一緻的。可以參考
v2.4: https://docs.opencv.org/2.4/modules/core/doc/operations_on_arrays.html#void%20log(InputArray%20src,%20OutputArray%20dst)
v3.4:
https://docs.opencv.org/3.4/d2/de8/group__core__array.html#ga937ecdce4679a77168730830a955bea7
總結起來就是3.4版本對于自變量出現負值、零、NaN和Inf的處理更符合對log( )函數預期。3.4版本中,log( )函數對自變量為負值、零、NaN和Inf的處理是“未定義”,是以強制使用者對上述情況做出處理,實際上我認為這确實提高了程式的健壯性和可調式性。
讨論完上述兩個問題,接下來是如何實作卷積運算。實際上卷積運算可以看作是一次圖像的虛化處理(smoothing)。使用Gaussian kernel作為卷積核時,就是對圖像進行Gaussian blur。這樣可以使用OpenCV提供的GaussianBlur( )函數進行處理。所需要特殊注意的是OpenCV的GaussianBlur( )函數預設提供對圖像邊界(border)的處理,其預設的邊界類型為BORDER_DEFAULT也就是BORDER_REFLECT_101。這個設計可見OpenCV源碼,所在位置為opencv2/core/base.hpp的268行。
我預計使用BORDER_ISOLATED,表示不使用邊界外的資料,但是ROI如何定義,OpenCV在GaussianBlur的文檔裡也沒有明确表達。我暫時就這樣使用了。
而關鍵的問題是原文并未說明進行卷積時,圖像的邊界如何處理。
進行Gaussian smoothing時,原文推薦使用過7x7的核,這在OpenCV的實作中是非常容易的,僅是GaussianBlur( )函數的一個參數。
卷積運算部分讨論後,最後就是原文式(6)的計算。實際上我最開始直接想到,式(6)實際上是運用兩幅單通道的灰階圖計算出了一個2D的直方圖。隻不過這個直方圖比較特殊,它的每個次元範圍都是0-256,并且分成了256份。這一點也在如下網頁的描述上得到了印證
How can I calculate the joint entropy of two images in Opencv: https://stackoverflow.com/questions/14898349/how-can-i-calculate-the-joint-entropy-of-two-images-in-opencv
于是式(6)的運算就變為在OpenCV中進行一次2D直方圖運算。OpenCV提供了calcHist( )函數。這個函數的channels參數的定義非常迷。經過幾次調試之後,可以确定當calcHist( )的輸入圖像為兩個單通道的灰階圖像時,channels定義為{0, 1},這表示使用第一幅圖像的第一個通道,和第二個圖像的第一個通道。然後剩下一個問題是與OpenCV自身的設計有關的,即所生成直方圖的資料type。OpenCV在這裡的處理也比較隐晦,經過測試,使用兩個CV_8UC1類型的灰階圖像,生成的直方圖的資料type為CV_32FC1,也就是單精度浮點數(float)。這是正确的方法,若生成直方圖仍使用某些整數類型,可能導緻類型的數值溢出。
以上便是對原文式(4)、(5)和(6)的讨論。
5 Entropy of a Single Image
為了最後計算得到mutual information值,仍然需要計算兩個圖像自身的entropy。這在原文中被推薦通過joint entropy得到。具體方法非常直接,即對2D的PI1,I2沿着行或列累加,得到兩個圖像各自的P。然後通過原文的式(7a)和(7b)求得各個圖像的entropy。這裡僅有一個問題,即式(7a)和(7b)中的n的取值。我認為仍然去整張圖像的像素數量。
OpenCV提供了直接進行這個工作的函數,reduce( )。使用reduce( )函數時,資料type使用的仍然是CV_32FC1。
6 Mutual Information
經過上述讨論,并結合原文中式(8a)、(8b)、(9a)和(9b)的說明,初步的互資訊計算已經可以進行了。但實際上現階段仍然需要假定一個disparity map。
使用目前自己搭建的一個custom stereo camera,對一個靜态的牆面進行拍攝,利用所獲得的圖像為例進行mutual information的計算。
左右相機的圖像如圖 1和圖 2所示。
圖 1 左圖像(縮放調整後)
圖 2 右圖像(縮放調整後)
計算所得到的互資訊圖像如圖 3所示,此時采用的是常量disparity map,所用的數值是随意選取的。為了能夠采用灰階圖像的形式顯示mutual information,這裡将每個位置上的數值進行了歸一化處理。經歸一化處理的浮點數Mat對象,OpenCV的imshow( )函數是能夠以灰階形式顯示的。若需要儲存一個灰階圖像,則需要将這個Mat對象與255相乘,而後才能正确儲存。
圖 3 Mutual information
從圖形上看,整體形貌與(Hirschmüller 2008)中的執行個體相接近,不同的是原文中圖形的y坐标都是朝上的,而預設的圖檔坐标系,y軸都是自上而下的。另外,當disparity map不夠理想時,mutual information的分布會出現如圖 3所示的沿對角線的彌散狀。當disparity map非常理想時,mutual information的圖形應該在對角線上出現高值(白亮)在遠離對角線處出現低值(暗淡)。較好的disparity map表示左圖和warped image之間的match非常好,大部分joint entropy都将出現在對角線上,最後形成的mutual information圖形,在對角線上應當能夠看到較為白亮的帶。這裡,進行了一個額外的測試,使用左圖替代右圖,即兩幅圖完全一樣。所生成的mutual information灰階圖如圖 4所示(此時disparity map為全零),可以看到,在圖像上确實出現了較亮的對角線帶。
圖 4 相同輸入圖像生成的mutual information圖像
後期會針對原文的算法進行進一步研究和複現,現在先做到這裡。
參考文獻
Hirschmüller, Heiko. 2008. “Stereo Processing by Semiglobal Matching and Mutual Information.” IEEE Transactions on Pattern Analysis and Machine Intelligence 30 (2): 328–41. https://doi.org/ 10.1109/TPAMI.2007.1166 .