算法思想
- 希爾排序算法思想
-
使用一個增量序列{t1,t2,t3,......tn},其中tn>....>t2>t1=1,其實這個增量序列也可以了解為
間距序列;
設有數組A[k],下标從0開始:
當增量為tn時,從數組首元素A[0]開始,此時距離首元素間隔為tn的元素是A[tn],下一個距離元素A[tn]
間隔為tn的元素是A[tn*2],依次類推,從首元素開始間隔為tn的所有元素,A[0],A[tn],A[2*tn]....
A[x*tn]構成了一個分組,其中x*tn<k;
從數組第二個元素A[1]開始,此時距離A[1]間隔為tn的元素是
A[1+tn],下一個距離元素A[1+tn]間隔為tn的元素是A[1+tn*2],依次類推,從首元素開始間隔為tn的所
有元素,A[1],A[1+tn],A[1+2*tn]....A[1+x*tn]構成了一個分組,其中1+x*tn<k;
重複上述步驟,數組中所有的元素都被分組後,然後對每一個分組進行一次插入排序
取增量為tn-1,重複上述步驟進行分組,然後對每一個分組進行一次插入排序,直到取增量為t1時,此時數
組中的元素大緻有序,在對整個數組進行一次插入排序,即可排序完成
-
-
算法圖解
使用希爾排序對4,5,8,2,3,9,7,1進行排序,此時采用增量序列為{1,2,3},
當增量為3時:
當增量為2時: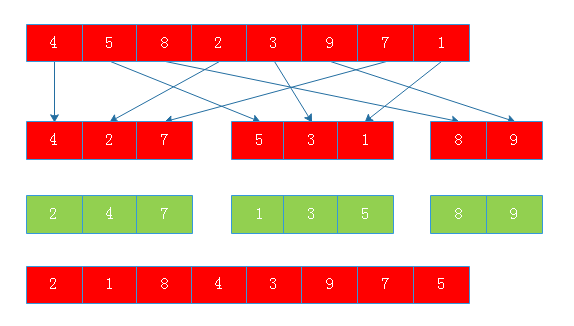
希爾排序 當增量為1時:希爾排序 可以看出當增量為1時,待排序元素已經大緻有序,此時進行一次插入排序即可完成排序希爾排序 -
增量序列的選取
希爾排序是否高效取決于增量序列的選取,計算機科學家Knuth在《the art of compute programming》
中提出當相鄰增量之間的比例為1:3時效果還行,也就是增量序列為{1,4,13,40,121,364,1093,.....}時
-
希爾排序和直接插入排序:
希爾排序是插入排序的擴充,插入排序每插入一次都要将插入位置以及它後面的元素整體向後進行一次平移,
例如,如果升序排序時,如果最小的元素在尾部,那麼就需要N次才能将其插入到數組的首元素位置,這期間要
進行多次移動,希爾排序通過允許非相鄰的等間距元素進行交換來減少插入排序頻繁挪動元素的弊端。
代碼實作
bool ShellSort(int * pUnSortAry, int nSize)
{
if (pUnSortAry == nullptr || nSize <= 0)
{
return false;
}
int nGrp = 0;
for (nGrp = 1; nGrp <= (nSize - 1) / 9; nGrp = nGrp * 3 + 1);
for ( ; nGrp >0; nGrp/=3)
{
for (int iIndex = nGrp; iIndex < nSize; iIndex++)
{
int nTemp = pUnSortAry[iIndex];
int jIndex = iIndex - nGrp;
for (; jIndex >= 0 && pUnSortAry[jIndex] > nTemp; jIndex -= nGrp)
{
pUnSortAry[jIndex+nGrp] = pUnSortAry[jIndex];
}
pUnSortAry[jIndex+nGrp] = nTemp;
}
}
return false;
}
測試代碼:
int main()
{
srand(time(NULL));
int nArry[30] = { 0 };
for (int jIndex = 0; jIndex < 10; jIndex++)
{
for (int iIndex = 0; iIndex < sizeof(nArry) / sizeof(nArry[0]); iIndex++)
{
nArry[iIndex] = rand() % 150;
}
printf("排序前:");
PrintData(nArry, sizeof(nArry) / sizeof(nArry[0]));
ShellSort(nArry, sizeof(nArry) / sizeof(nArry[0]));
printf("排序後:");
PrintData(nArry, sizeof(nArry) / sizeof(nArry[0]));
}
return 0;
}
測試結果:
穩定性
希爾排序是将等距離的元素分為一組,相同的元素可能會被分到不同的組,在一個分組中的插入排序是文檔的,
但是在多個分組多次插入排序的情況下可能會改變相同元素的相對位置,是以希爾排序是不穩定的排序