目录
- 题目要求
- 公式推导和计算
- 计算流程图
- pyhton代码
- 生成图表一览
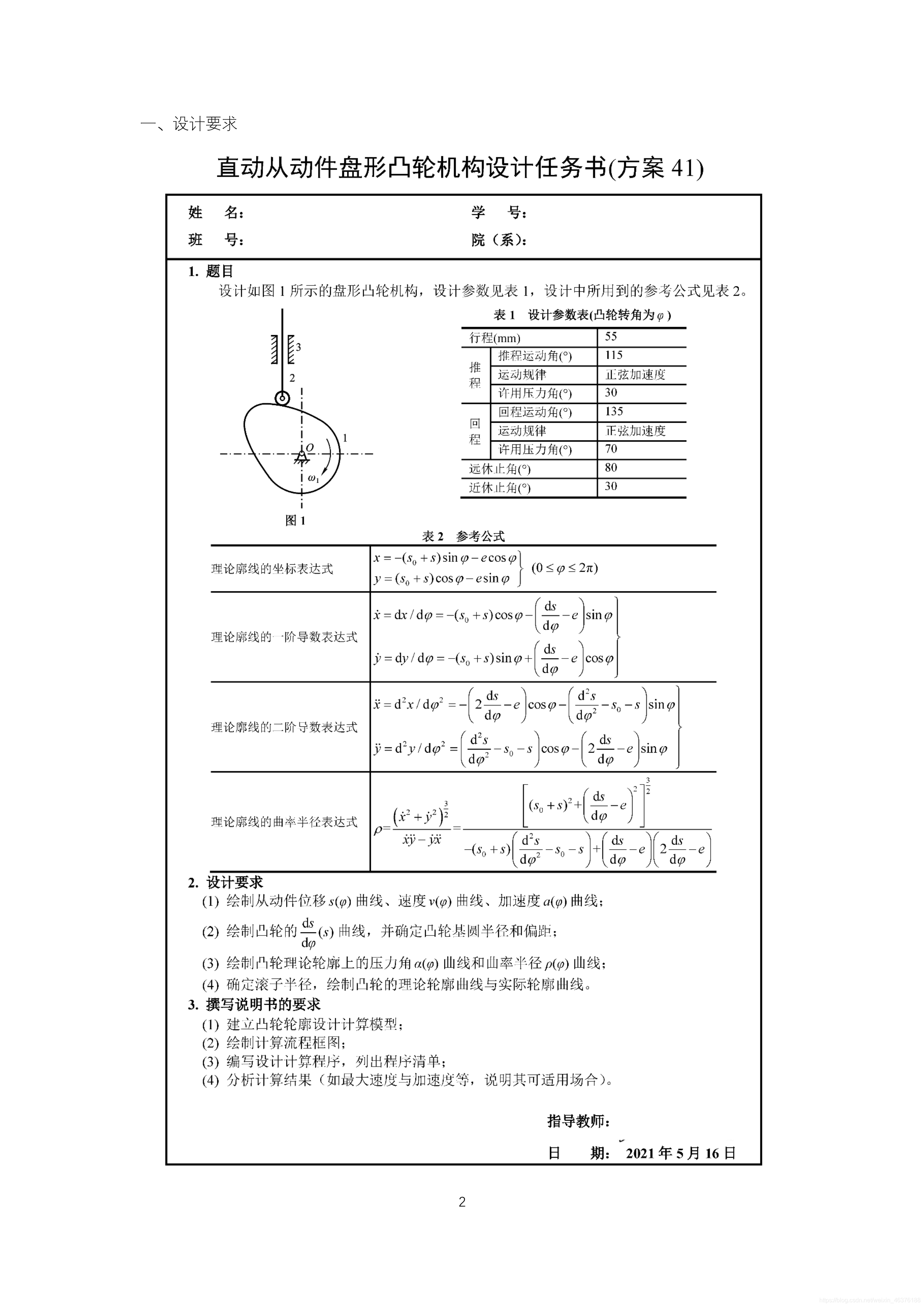
题目要求
公式推导和计算
计算流程图
pyhton代码
from abc import ABCMeta, abstractmethod
from mpl_toolkits import axisartist
import math
from matplotlib import pyplot as plt
import matplotlib.font_manager as font_manager
from matplotlib.pyplot import MultipleLocator
import numpy as np
class travel():
__mata_class_=ABCMeta
def __init__(self,**kwargs):
self.h=kwargs.get("h")
self.Phi=kwargs.get("Phi")
@abstractmethod
def state_phi(self):
pass
class sin_travel(travel):
def __init__(self,**kwargs):
super().__init__(**kwargs)
self.push_travel=kwargs.get("push_travel")
def state_phi(self,phi):
Phi=self.Phi*math.pi/180
phi=phi*math.pi/180
if (self.push_travel):
return [self.h*(phi/Phi-math.sin(2*math.pi*phi/Phi)/(2*math.pi)),
self.h*(1-math.cos(2*math.pi*phi/Phi))/Phi,
self.h*2*math.pi*math.sin(2*math.pi*phi/Phi)/Phi**2]
else:
return [self.h*(1-phi/Phi+math.sin(2*math.pi*phi/Phi)/(2*math.pi)),
-self.h*(1-math.cos(2*math.pi*phi/Phi))/Phi,
-self.h*2*math.pi*math.sin(2*math.pi*phi/Phi)/Phi**2]
class pause_travel(travel):
def state_phi(self,phi):
return [self.h,0,0]
class cam():
def __init__(self,Law_of_motion:list,**kwarg):
self.travel=Law_of_motion
self.e=kwarg.get("e")
self.r_0=kwarg.get("r_0")
self.r_r=kwarg.get("r_r")
self.omega=kwarg.get("omega")
if(self.r_0!=None and self.e!=None):
self.s0=math.sqrt(self.r_0**2+self.e**2)
#求位移类速度类加速度
def get_motion_state_phi(self,phi)->list:
i=0
while(phi>self.travel[i].Phi):
phi-=self.travel[i].Phi
i+=1
return self.travel[i].state_phi(phi)
def get_motion_state(self,phi)->list:
def tf(i):
i+=1
return i-1
i=0
return list(map(lambda x:x*self.omega**tf(i),self.get_motion_state_phi(phi)))
def get_pressure_angle(self,phi):
state_phi=self.get_motion_state_phi(phi)
return math.atan(abs(state_phi[1]-self.e)/\
(self.s0+state_phi[0]))*180/math.pi
def get_theoretical_outline(self,phi)->tuple:
t=self.s0+self.get_motion_state_phi(phi)[0]
phi=phi*math.pi/180
return (-t*math.sin(phi)-self.e*math.cos(phi),
t*math.cos(phi)-self.e*math.sin(phi))
def get_theoretical_outline_dphi(self,phi)->tuple:
state=self.get_motion_state_phi(phi)
t1=self.s0+state[0]
t2=state[1]-self.e
phi=phi*math.pi/180
return (-t1*math.cos(phi)-t2*math.sin(phi),
-t1*math.sin(phi)+t2*math.cos(phi))
def get_theoretical_outline_ddphi(self,phi)->tuple:
state=self.get_motion_state_phi(phi)
phi=phi*math.pi/180
t1=2*state[1]-self.e
t2=state[2]-self.s0-state[0]
return (-t1*math.cos(phi)-t2*math.sin(phi),
-t1*math.sin(phi)+t2*math.cos(phi))
def get_rho(self,phi):
(dx,dy)=self.get_theoretical_outline_dphi(phi)
(ddx,ddy)=self.get_theoretical_outline_ddphi(phi)
return math.sqrt(dx**2+dy**2)**3/(dx*ddy-dy*ddx)
def get_partical_outline(self,phi)->tuple:
t=math.sqrt(self.get_theoretical_outline_dphi(phi)[0]**2+\
self.get_theoretical_outline_dphi(phi)[1]**2)
t1=self.get_theoretical_outline_dphi(phi)[1]/t
t2=self.get_theoretical_outline_dphi(phi)[0]/t
return (self.get_theoretical_outline(phi)[0]-self.r_r*t1,\
self.get_theoretical_outline(phi)[1]+self.r_r*t2)
def set_co_axis(ax:axisartist.Subplot,title="",xlabel="",ylabel="",pxl=(0,0),pyl=(0,0)):
ax.axis[:].set_visible(False)
ax.axis["x"] = ax.new_floating_axis(0,0)
ax.axis["x"].set_axisline_style("->", size = 1.0)
ax.axis["y"] = ax.new_floating_axis(1,0)
ax.axis["y"].set_axisline_style("-|>", size = 1.0)
ax.axis["x"].set_axis_direction("top")
ax.axis["y"].set_axis_direction("right")
ax.set_xticks([ 0, np.pi/2, np.pi, 3*np.pi/2, 2*np.pi])
ax.set_xticklabels([ "", 'π/2', 'π', '3π/2', '2π' ])
ax.text(pxl[0],pxl[1],xlabel,ha="center",va="center")
ax.text(pyl[0],pyl[1],ylabel,ha="center",va="center")
ax.set_title(title)
if (__name__=="__main__"):
h=55
Phi_0_1=115
Phi_0_2=135
Phi_s_1=80
Phi_s_2=30
alpha_1=30
alpha_2=70
omega=1
Law_of_motion=[sin_travel(h=h,Phi=Phi_0_1,push_travel=True),
pause_travel(h=h,Phi=Phi_s_1),
sin_travel(h=h,Phi=Phi_0_2,push_travel=False),
pause_travel(h=0,Phi=Phi_s_2)]
Cam=cam(Law_of_motion,omega=1)
mo_data=[[],[],[]]
mo_dphi_data=[[],[],[]]
for i in range(0,360):
mo_dphi_data=list(map(lambda x,y:x+[y],
mo_dphi_data,Cam.get_motion_state_phi(i)))
mo_data=list(map(lambda x,y:x+[y],
mo_data,Cam.get_motion_state(i)))
y1=mo_dphi_data[0][i]-math.tan((90-alpha_1)*math.pi/180)*mo_dphi_data[1][i]
y2=mo_dphi_data[0][i]-math.tan((90+alpha_2)*math.pi/180)*mo_dphi_data[1][i]
if (i==0):
py1,py2,f1,f2=y1,y2,0,0
else:
if(f1!=-1):
if(f1==1 and py1<y1):
f1,s_1,x_1=-1,mo_dphi_data[0][i-1],mo_dphi_data[1][i-1]
elif(f1==0 and y1<py1):
f1=1
py1=y1
if(f2!=-1):
if(f2==1 and py2<y2):
f2,s_2,x_2=-1,mo_dphi_data[0][i-1],mo_dphi_data[1][i-1]
elif(f2==0 and y2<py2):
f2=1
py2=y2
fig1=plt.figure(figsize=(10,10),dpi=80)
phi_x=np.linspace(0,2*math.pi,360)
s_phi=axisartist.Subplot(fig1,3,1,1)
v_phi=axisartist.Subplot(fig1,3,1,2)
a_phi=axisartist.Subplot(fig1,3,1,3)
s_phi.plot(phi_x,mo_data[0])
v_phi.plot(phi_x,mo_data[1])
a_phi.plot(phi_x,mo_data[2])
set_co_axis(s_phi,"s(φ)","φ","s",(2.15*math.pi,3),(0.1,60))
set_co_axis(v_phi,"v(φ)","φ","v",(2.15*math.pi,3),(0.1,65))
set_co_axis(a_phi,"a(φ)","φ","a",(2.15*math.pi,3),(0.1,100))
fig1.add_axes(s_phi)
fig1.add_axes(v_phi)
fig1.add_axes(a_phi)
X_Phi=[0,Phi_0_1,Phi_0_1+Phi_s_1,Phi_0_1+Phi_s_1+Phi_0_2,360]
for i in range(0,4):
a_phi.arrow((X_Phi[i+1]+X_Phi[i])*math.pi/360, -100,
(X_Phi[i+1]-X_Phi[i])*math.pi/360, 0,
width=0.01,
length_includes_head=True,
head_width=3,
head_length=0.1,
fc='r',
color='b',
ec='b')
a_phi.arrow((X_Phi[i+1]+X_Phi[i])*math.pi/360, -100,
-(X_Phi[i+1]-X_Phi[i])*math.pi/360, 0,
width=0.01,
length_includes_head=True,
head_width=3,
head_length=0.1,
fc='r',
color='b',
ec='b')
for X in [Phi_0_1,Phi_0_1+Phi_s_1,Phi_0_1+Phi_s_1+Phi_0_2,360]:
a_phi.plot([X*math.pi/180,X*math.pi/180],[-105,0],c="black",linewidth=1)
a_phi.text((X_Phi[0]+X_Phi[1])*math.pi/360,-108,r"$Φ_0$",ha='center',va='center')
a_phi.text((X_Phi[2]+X_Phi[1])*math.pi/360,-108,r"$Φ_s$",ha='center',va='center')
a_phi.text((X_Phi[2]+X_Phi[3])*math.pi/360,-108,r"${Φ_0}^{'}$",ha='center',va='center')
a_phi.text((X_Phi[3]+X_Phi[4])*math.pi/360,-108,r"${Φ_s}^{'}$",ha='center',va='center')
fig2=plt.figure(figsize=(10,10),dpi=80)
ds_dphi_s=axisartist.Subplot(fig2,1,1,1)
set_co_axis(ds_dphi_s,"","ds/dφ","s",(67,3),(3,65))
ds_dphi_s.set_xticks(np.linspace(-40,60,11))
ds_dphi_s.set_yticks(np.linspace(-100,60,17))
x1=np.linspace(0,60,600)
x2=np.linspace(-50,50,1000)
x3=x1
s1=math.tan((90-alpha_1)*math.pi/180)*(x1-x_1)+s_1
s2=math.tan((90+alpha_2)*math.pi/180)*(x2-x_2)+s_2
s3=-math.tan((90-alpha_1)*math.pi/180)*x3
ds_dphi_s.plot(mo_dphi_data[1],mo_dphi_data[0])
ds_dphi_s.plot(x1,s1)
ds_dphi_s.plot(x2,s2)
ds_dphi_s.plot(x3,s3)
ds_dphi_s.text(67,3,"ds/dφ",ha="center",va="center")
ds_dphi_s.text(3,65,"s",ha="center",va="center")
e=-(s_1-math.tan((90-alpha_1)*math.pi/180)*x_1)/(2*math.tan((90-alpha_1)*math.pi/180))
s_0=(s_1-math.tan((90-alpha_1)*math.pi/180)*x_1)/2
ds_dphi_s.plot(e,s_0,marker='o')
ds_dphi_s.annotate("(%.2f,%.2f)" % (e,s_0),
xy=(e,s_0),
xytext=(5,0),
textcoords='offset points')
ds_dphi_s.set_aspect(1)
ds_dphi_s.grid()
fig2.add_axes(ds_dphi_s)
Cam.e,Cam.s0,Cam.r_0=e,-s_0,math.sqrt(e**2+s_0**2)
alpha_data=[]
rho_data=[]
for i in range(0,360):
alpha_data.append(Cam.get_pressure_angle(i))
rho_data.append(Cam.get_rho(i))
if(i==0 or (rho_data[i]>0 and rho_data[i]<rho_min)):
rho_min=rho_data[i]
fig3=plt.figure(figsize=(10,10),dpi=80)
alpha_phi=axisartist.Subplot(fig3,2,1,1)
rho_phi=axisartist.Subplot(fig3,2,1,2)
set_co_axis(alpha_phi,R"e=%.2f $r_0$=%.2f"%(e,math.sqrt(e**2+s_0**2)),
"φ","α",(2.15*math.pi,0.5),(0.1,53))
set_co_axis(rho_phi,'ρ(φ)',"φ","ρ",(2.15*math.pi,0.5),(0.1,1200))
alpha_phi.plot(phi_x,alpha_data)
rho_phi.plot(phi_x,rho_data)
fig3.add_axes(alpha_phi)
fig3.add_axes(rho_phi)
Cam.r_r=rho_min*0.4
x_data=[]
y_data=[]
px_data=[]
py_data=[]
for i in range(0,360):
x_data.append(Cam.get_theoretical_outline(i)[0])
y_data.append(Cam.get_theoretical_outline(i)[1])
px_data.append(Cam.get_partical_outline(i)[0])
py_data.append(Cam.get_partical_outline(i)[1])
fig4=plt.figure(figsize=(10,10),dpi=80)
x_y=plt.subplot(1,1,1)
x_y.set_aspect(1)
x_y.grid()
x_y.xaxis.set_major_locator(MultipleLocator(10))
x_y.yaxis.set_major_locator(MultipleLocator(10))
l1,=x_y.plot(x_data,y_data,label="理论廓线",linestyle='--')
l2,=x_y.plot(px_data,py_data,label='实际廓线')
x_y.set_title(r'${ρ}_{min}=$'+'%.2f\n'%(rho_min)+r'${r}_{r}={ρ}_{min}*0.4=$'+'%.2f\n'%(rho_min*0.4))
font=font_manager.FontProperties(fname='C:\Windows\Fonts\simsun.ttc')
fig4.legend(handles=[l1,l2],labels=['理论廓线','实际廓线'],loc=[0.15,0.72],prop=font)
fig4.add_axes(x_y)
plt.show()
生成图表一览