层次聚类算法介绍

• 1层次聚类的定义
• • 思考示例问题：
• 2距离与相似性
• • 2.1常用的计算距离的方法
  • 2.2计算指标相似性的方法
  • • 1)余弦计算公式：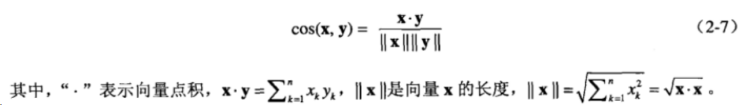
    • 2)相关计算公式：
• 3合并算法思想
• • • 1)重心法
    • 2)最短距离法
    • 3)最长距离法
    • 4)组间平均连接法
    • 5)组内平均链接法
• 4算法流程
• • • 程序执行过程：
• 5 示例与分析
• • 5.1基于最小值的层次聚类
  • • 优缺点
  • 5.2 基于最大值的层次聚类
  • • 优缺点
  • 5.3基于组平均
  • • 优缺点 （MIN和MAX之间的折中）
• 6需注意的问题
• • • 对比Kmean算法

1.本博客是观看清风数学建数学建模课程后有所感想记录的笔记，有想要深入学习的朋友可以购买观看课程：https://weidian.com/?userid=1372657210

2.感兴趣的推荐看B站数学建模试看课程：

https://www.bilibili.com/video/av20238704

1层次聚类的定义

聚类就是对大量未知标注的数据集，按照数据内部存在的数据特征将数据集划分为多个不同的类别，使类别内的数据比较相似，类别之间的数据相似度比较小，属于无监督学习。

层次聚类的合并算法通过计算两类数据点间的距离，对最为接近的两类数据点进行组合，并反复迭代这一过程，直到将所有数据点合成一类，并生成聚类谱系图。

思考示例问题：

2距离与相似性

2.1常用的计算距离的方法

Ps：其中绝对值距离一般应用于网状道路距离，一般采用欧氏距离。

2.2计算指标相似性的方法

1)余弦计算公式：

2)相关计算公式：

3合并算法思想

思想：将两个簇合成为一个簇，计算这个簇与其他簇之间的距离，再进行合并。

簇与簇之间的常用距离：重心法，最短距离法，最长距离法，组间平均连接法，组内平均链接法（下图顺序一致）

1)重心法

2)最短距离法

3)最长距离法

4)组间平均连接法

5)组内平均链接法

4算法流程

程序执行过程：

系统(层次)聚类的算法流程:
	1.将每个对象看作一类，计算两两之间的最小距离;
	2.将距离最小的两个类合并成一个新类;
	3.新计算新类与所有类之间的距离;
	4.重复2、3两步，直到所有类最后合并成一类;
	5.结束。
           

5 示例与分析

根据所给的图，以及距离矩阵，求解聚类结果：

5.1基于最小值的层次聚类

计算结果如下：

优缺点

优点：可以处理非椭圆形状

缺点：对噪声点和异常值敏感

5.2 基于最大值的层次聚类

计算结果如下：

优缺点

优点：不容易受噪声点和异常值影响

缺点：1.往往打破大聚类 2.偏向球状星团

5.3基于组平均

计算结果如下：

优缺点 （MIN和MAX之间的折中）

优点：不易受噪声和异常值影响

缺点：偏向球状星团

6需注意的问题

1.对于一个实际问题要根据分类的目的来选取指标，指标选取的不同分类结果一般也不同。
2.样品间距离定义方式的不同，聚类结果一般也不同。
3.聚类方法的不同，聚类结果一般也不同 (尤其是样品特别多的时候)。最好能通过各种方法找出其中的共性。
4.要注意指标的量纲，量纲差别太大会导致聚类结果不合理。
5.聚类分析的结果可能不令人满意，因为我们所做的是一个数学的处理，对于结果我们要找到一个合理的解释。
           

对比Kmean算法

k均值需要定义聚类簇数k，而层次聚类不需要，层次聚类可以根据聚类谱系图选择聚类的簇个数。